Self Propelled Aeroplane with Automatic Equilibrium

Alphonse Penaud

L’Aeronaute, January 1872

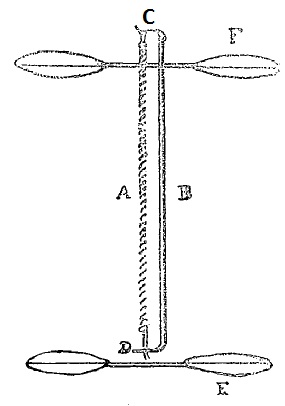
At the end of April 1870, I presented to M. de La Landelle and our honorable General Secretary, Mr. Huréau de Villeneuve, a small motor helicopter based on the untwisting force of one or more rubber bands previously twisted around themselves. This helicopter consists of a propeller F fixed to a wooden rod B, and a moving propeller E. Rod B has at its upper end a hook C to which is attached a rubber band A, whose lower end is attached to the shaft of propeller E mounted on the bearing D. When one wants to fly the device, propeller E is rotated in the direction contrary to that of useful rotation, thus twisting the rubber band, which, when released, turns the moving propeller directly and the other propeller by reaction.

 

Fig. 1. Self propelled helicopter.

This small model, described in l’Aeronaute, August 1870, flies much longer than the historical apparatus of M. Ponton d’Amécourt. The reason for this superiority is in the employment of rubber instead of spring steel.

A steel spring weighing 1 kilogram can store no more than 10 kilogram meters of energy. The same weight of rubber stretched to six times its natural length, provides, by shortening, 500 kilogram meters, or fifty times more work. The benefit resulting from the use of the latter substance is enormous. It should be noted however, that tension requires, for its use, a more or less complicated mechanism, absorbing part of the force, requiring very great precision, and difficult to make both strong and light.

So, seeking to use the extraordinary strength of rubber in a really simple way, I had the idea of using its torsional elasticity, which can provide 130 kilogram meters per kilogram. This figure is, in fact, much lower than the previous, but for a very precise mechanism, this inferiority is largely compensated by the wonderful ease with which the twist is applied to the rotating propeller. Any movement transformation is avoided, the frames become extremely simple and light, almost no friction, the effort finally has the remarkable distinction of not growing nearly as fast as the number of turns. All circumstances eminently favorable to good use.

After having varied the proportions of my helicopter, after seeing it fly up, hovering sideways, rising like an arrow, naturally the thought occurred to me to apply my mechanism to propel an airplane type apparatus in order to show the ability of this system demonstrated by the helicopter to power the propeller.

But I was stopped by a big difficulty, equilibrium. Without equilibrium, the device would be unable to provide the least flight, it would fall to earth, despite its propulsion and inclined plane. Fortunately, after some research, I imagined a very simple device, filling the desired purpose.

It is a small horizontal governor tilted below the sustaining plane, behind which it is located. This device may ultimately be related to the property that surfaces convex downward fall vertically without capsizing, and with which Mr. Joseph Pline even managed to build pretty little butterflies which glide obliquely to the ground. But in my airplane there is, as in the bird, a complete separation of the supporting surface and the regulating surface, with which unimpaired translation is more easily made, and finally, my governor is obviously a better steering device to provide on an air vessel controlled by a man.

Anyway, the theory of a fixed governor automatically regulating the level of the device, not having been exposed nor even considered by anyone to my knowledge, I will treat here in a few words:

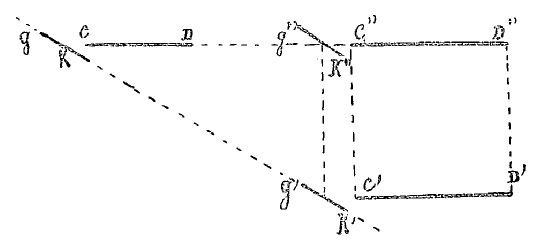
Fig. 2. Automatic governor.

In Fig. 2, CD is a horizontal plane carrying weight positioned below the center of pressure, and connected to a governor GK downwardly inclined below its surface. Suppose that it moves horizontally with a certain speed, which leads to C”D” after a given time. During this same time, it will be dropped under gravity a certain amount, C”C’, depending on the size of surface and weight of the load, so that ultimately CD is at the end of the given time at C’D’, and therefore GK is at G’K’; and we may conceive that providing a suitable value for translation speed, the vertical drop and finally the angle of the governor plane, G’K’ can ultimately be on the extension of GK, as shown in the figure, so that the real movement is that it will cleave the air by its edge. Suppose now that CD inclines slightly down to the ground, its speed will increase, since the propulsive force will join a component of its weight, but then, for the same drop C”C’, the horizontal path will be greater, the final position of CD and hence GK will be to the right of C’D’, G’K’. The governor will therefore receive the impact of the air on the top, it will be pushed down. As the device tends to rotate around its center of gravity, the front will rise, and plane CD will resume its horizontal position. If on the contrary the plane tends to rise, it immediately slows its speed, the governor receives air on its bottom which returns CD to its natural position, so that the device is forced to descend in the direction GG’.

If one supposes that CD, instead of being absolutely horizontal, is inclined slightly upward or downward from its normal position, you can see with a little attention, that the governor will have the same effects, so that either a horizontal, uphill or downhill flight at a prescribed angle is obtainable thereby. One can even get all these effects by shifting part of the weight to the governor itself, placing the center of gravity a bit backwards. The supporting surface is increased, which is advantageous.

As for lateral balance, it is sufficient, to obtain it, to slightly tilt the wings upwards, or simply raise their tips.

Finally, I do not use a single blade propeller. It is recognized, rightly, that an air vessel must have an even number of blades, two by two, equal and not otherwise, since only one propeller blade tends to turn the device on itself. However, having done some calculations about it, I realized it was just possible to employ a propeller of larger diameter without significantly reducing the run of the air supplied. Therefore, I adopted in my device this provision that simplifies both the construction and handling while making it stronger.

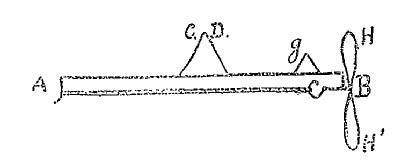
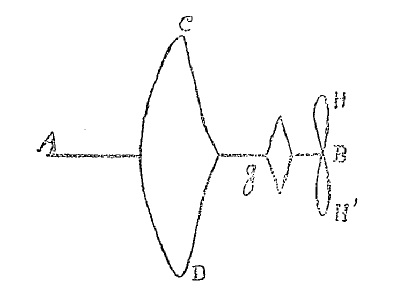
Fig. 3. Aeroplane in elevation.

My aeroplane, that I also call Planophore, consists of a rod AB 50 centimeters long, with a short lug at A and a small bearing at B, through which the shaft of the propeller HH’ passes. This shaft is terminated by a hook to which is attached the end of a rubber band attached at the other end to the lug A. Propeller HH’ is 21 centimeters in diameter. It has only two blades, so that upon reaching the ground, it can be placed flat on the soil and not continue to turn, as do propellers with several blades, which can deteriorate and break. In addition, the weight of the propeller is concentrated on two blades, that are naturally stronger. From the point of view of flight, the propeller with four blades should be better.

Fig. 4. Aeroplane in plan.

Towards the middle of the rod AB is a plane CD 45 centimeters long, about 11 centimeters wide. Ends C and D are slightly raised and receive a light curve which contributes to prevent capsizing to the side. This form stretched out abeam, excellent for support, is also very useful to maintain straight motion. Thus, in certain birds, we see long wings almost entirely compensate the tail, while birds with large wings all have a considerable tail.

Before the propeller is the governor G, with a similar shape to the great plane and having like it upturned ends.

The lateral direction is obtained by a small vertical governor acting as on ships.

The center of gravity is slightly forward of the center of the surface CD. The assembly weighs 16 grams, of which the rubber accounts for 5 grams. So it seems difficult to adapt significantly greater engine power in a lighter frame.

Now, if after turning the propeller about 240 times, the Planophore is released in a horizontal position, we see it descend a moment, then it acquires speed, rises up and describes a regular movement, seven or eight feet from the ground, a course of about 40 meters, and lasting 11 seconds. I’ve even seen it circling up to 60 meters for 13 seconds.

During this time, the governor suppresses ascending or descending inclinations as they occur, with perfect accuracy, and there are often oscillations in flight, as we see in sparrows and mainly woodpeckers. Finally, when the movement is at its end, the apparatus falls gently to the ground, in an oblique line, remaining perfectly upright.

Several members of the Society wished to attend the experiment, August 18, and the smaller model has traveled one of the roundabouts of the Tuileries Gardens several times in their presence.

Average speed of 3.6 meters per second is quite similar to the regular speed of insects which have the same ratio of weight to wing area, such as dragonflies and some grasshoppers. This is the highest speed that propelled aerial equipment has yet reached, rockets, of course, excepted. This speed is naturally slowed by a headwind and can even become negative if the wind is a bit strong. On the contrary, if the wind is favorable, the flight is accelerated as much, and I have often seen it acquire considerable speed. Finally, if the wind speed is exactly equal to that of the Planophore, it will remain in place in space, as some birds. I had several opportunities to observe this interesting fact, and I learned a way to measure the work expended in one second.

Everything being arranged in the most advantageous way known, I saw that the propeller should be wound to 60 turns so the small model could stand for a moment in the air, without dropping or retreating, against a wind of 2.7 meters per second. It then flew obviously by itself, the wind making only at the outset, the conditions of normal speed it may acquire in calm air.

The speed of rotation of the propeller was 18 revolutions per second and the torque of the propeller 2.9 grams X 10 centimeters. I had the total power expended, 18 X 2.9 X 2 π 10 = 32.8 gram meters per second as the power required to raise the total weight of 16 grams 2.05 meters in one second, which corresponds to one horse power per 37 kilograms.

This is the total power. But I thought it would be equally interesting to see how much the suspension, propeller and transmission absorb respectively. This can be achieved approximately as follows:

1. The work expended by the suspension is the work of the resistance of the air on the sustaining plane. The vertical component of this resistance is known, it is the 16 grams weight of the apparatus. The horizontal component is equal to the first multiplied by the tangent of the angle of the plane with the horizon. Yet this is precisely the angle formed by the governor and sustaining plane. If the center of gravity is placed just below the center of pressure of the latter, this angle is 8°. Work sought is the product of effort by the path, that is to say the speed of the wind, power is therefore 16 grams X tan(8°) X 2.7 meters per second = 6.1 gram meters per second.

Here, 16 grams are supported by 490 square centimeters of surface. According to this, 1 square meter moving at the same angle 8°, at the speed of 1 meter per second, experiences a supporting resistance of 45 grams, a figure actually too low, because the curve of the plane prevents it from acting with all possible efficiency. However, it is still at least 10 times more than is supposed by Navier.

2. Losses due to the propeller are from two causes: slip and friction.

To get the power lost due to friction, I placed the blades flat in a plane perpendicular to the axis and I spun them at the speed with which they cut through the air in the real flight. The power expended in these conditions, 5 gram meters per second, is substantially equal to that which we seek.

To get slip, we need to know pitch, 32 centimeters, and the speed and the number of revolutions given above. It is therefore:

Slip: (18 revolutions per second X 32 centimeters per revolution – 270 centimeters per second) / 18 revolutions per second X 32 centimeters per revolution = 0.53.

Work absorbed by the slip is essentially 0.53 of the total work as reduced by friction, or 14.7 gram meters per second.

3. Finally, the work of transmission is the difference between the total work and the amount of previous work, 7 gram meters per second.

Total power available 32.8 gram meter per second

Propeller friction loss -5.0

                                   27.8

Propeller slip loss     -14.7

                                   13.1

Suspension loss          -6.1

Transmission loss         7.0

So we see that the great cause of expense is the propeller. We gain little by increasing the sustaining plane to reduce the suspension work, while there would be a great advantage from improving the propeller in order to reduce slip. All these results are only approximate, the data themselves are not known precisely, and also can not be, given the flexibility of the various parts and their smallness, but they tell us roughly the role of each member and the general conditions to be fulfilled by large aeroplanes. This shows well that often we need not go too much further than to take advantage of the simplest facts and experiments.

Anyway, my Planophore demonstrates the possibility of the aeroplane system, the possibility of a stable equilibrium in the air, and promises, to large apparatus, a considerable speed.

A. Penaud