Many discussions of the lift on a wing appeal to the Bernoulli principle. It is said that the air going over the top of the wing must go farther than the air going under the wing and to get to the trailing edge in the same time it must go faster. We are told that according to the Bernoulli principle, where the velocity is high, the pressure is low. The higher pressure underneath and the lower pressure above produces the lift on the wing. Actually Bernoulli’s principle has absolutely nothing whatsoever to do with the lift on a wing. It is based on assumptions which directly contradict the possibility of flight.

D’Alembert’s Proof

In the pioneer years of aviation, journalists would ask experts, physicists with PhD degrees and Nobel Prizes in physics, what they thought about flying machines and the universal response was something to the effect that “Mechanical flight is physically and mathematically impossible.” There is a mathematical proof, based on the Bernoulli principle, that a body moving through an ideal fluid would experience no resultant force. The Bernoulli principle is part of the classical theory of ideal fluids which is based on rational, logical postulates which are wrong when applied to real air. The ideal fluid is postulated to be continuous and frictionless. Air has very different properties than those postulated for the ideal fluid. The Bernoulli principle makes the rational assumption that energy is conserved in a moving fluid. For a force to exist on a moving object requires a transfer of energy, energy is not conserved in the fluid. The Bernoulli ideal fluid is continuous and frictionless. D’Alembert showed in 1752 that no such force could exist in the ideal fluid.

Circulation Theory

Prandtl proposed the circulation theory of flow around a wing, following observations by Rayleigh, Lanchester and Montgomery. This provided a theory that was in agreement with observation at least for small angles of attack. It gave no explanation of how the circulation came into being or what determined its strength. (L. Prandtl and O. G. Tietgens, Applied Hydro- and Aeromechanics, Dover Publications, New York, 1934, 1957. Chapter VI, Airfoil Theory.) The pattern of flow around a wing and the resulting forces derive from the molecular nature of real fluids. Real fluids are made of molecules that jiggle around at random with what is known as Brownian motion. This random jiggling permits transfer of momentum within a fluid. It creates the shearing forces that create circulation. It is the physical condition of the forces around the sharp trailing edge that determine the Kutta condition that defines the circulation strength that produces lift. (L. Prandtl and O. G. Tietgens, Applied Hydro- and Aeromechanics, Dover Publications, New York, 1934, 1957. Fig. 42-55, pages 296-301.)

False Assumptions

The usual discussion contains a misstatement and misapplication of the Bernoulli principle. The principle applies to two cross sections of a single fluid stream in steady flow. It says the total energy will be the same at both cross sections. It is not valid to compare two different fluid flow streams or a moving stream with ambient static air. The assumption that “the oncoming airflow traveling over the upper surface has a greater distance to travel in the same amount of time than the lower air flow, so it travels faster” is simply not true, there is no basis for this statement other than ignorant assumption. In fact, as has been observed in wind tunnels, the two particles of air that separate at the leading edge do not arrive at the trailing edge at the same time. By the time the lower particle arrives at the trailing edge, the upper particle may have gone another 50% of the wing chord farther, as Dr. Lippisch shows in the linke video at 22:40-23:29. Also here.

False Conclusions

Also, if you attempt to apply this form of the Bernoulli principle, you will get an absurd result. Applying the transit time/velocity calculation to the Clark Y airfoil tells us that the Spirit of St.Louis could not have got airborne at anything like the speeds it flew. This is an exercise anybody can do, at home or in a classroom.

I printed a profile drawing of the Clark Y airfoil and taped it to a building board. I stuck pins along the curves, closer together in the more tightly curved areas, so the curve was sensibly straight between pins. I tied an 8 knot in some Dacron fishing line and stuck the pin from the leading edge through the knot.

I pulled the line tightly against the pins along the upper curve.

I pulled the line tightly against the trailing edge pin and marked the location with a pencil.

I pulled the line along the lower curve and marked the position of the trailing edge.

I measured the distance from the knot to the two pencil marks. The distance over the top was 8.82″ and the distance along the bottom was 8.60″. If you have a model airplane wing, you can do something similar with a strip of paper.

This misapplication of the Bernoulli principle says the ratio of the velocities must be in the ratio of the lengths.

The form of the Bernoulli equation which applies here is

Pt + ½ ρ Vt² = Pb + ½ ρ Vb²

where

Pt= pressure over the top surface in pounds per square foot

Pb= pressure on the bottom surface in pounds per square foot

Vt = velocity over the top in feet per second

Vb = velocity under the bottom in feet per second

ρ = air density 0.002378 slugs per cubic foot

From the proportionality of the lengths we get the ratio of the velocities

Vt/Vb = 8.82/8.60 = 1.02558 and Vt = Vb x 1.02558

Rearranging the Bernoulli equation, we get

Pb – Pt = ½ ρ (Vt² – Vb²) = ½ ρ (1.02558² – 1) Vb² = ½ ρ (0.05181) Vb²

The Spirit of St. Louis used the Clark Y airfoil. It had a takeoff weight of 5,135 pounds, a wing area of 320 square feet and a cruise speed of 100-110 miles per hour. The wing loading, equal to the difference between the bottom pressure and the top pressure, was 16 pounds per square foot. Thus we get

Pb – Pt = ½ ρ (0.05181) Vb² = 16

Solving for Vb gives us Vb = 509.6 feet per second = 347.5 miles per hour and Vt = 356.3 miles per hour, well above the actual flight speed of the airplane. From the lift equation

L = ½ S ρ Vb² Cl

We can find the lift coefficient corresponding to this speed, Cl = 0.05196, where

L = lift in pounds

S = wing surface area in square feet

The Spirit of St.Louis flew at a lift coefficient of about 0.54.

Contradicted by Wind Tunnel Measurements

This application of the Bernoulli principle also contradicts the well known observation that the lift on a wing is approximately linearly related to the attack angle, where the transit path theory postulates that the lift is not dependent on the attack angle at all, but only the path lengths. Wind tunnel measurements even show a negative lift for negative attack angles.

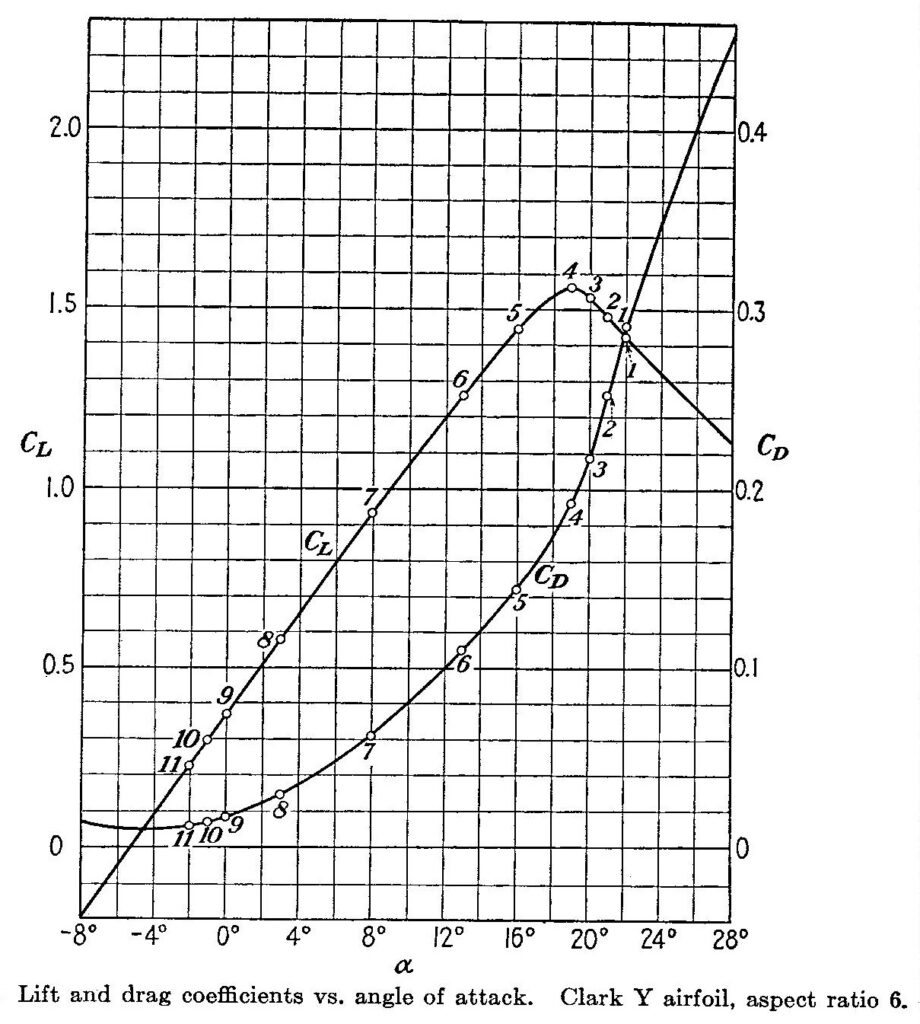
It also fails to say anything at all about the important drag component of the force. This application of the Bernoulli principle also does not account for the varying pressure distribution over the surface of the airfoil, which the circulation theory does.

Doesn’t Work for Thin Wings

The Bernoulli principle also does not work for a flat plate or thin cambered wing, where the circulation theory does. Many kites have flat airfoils. Many model gliders and airplanes have flat or thin cambered wings where the distance over the top is exactly the same as the distance along the bottom.

Doesn’t Work for Inverted Flight

It is common for aerobatic planes to fly inverted. If the unequal distance theory was correct, this would not be possible.

A False Demonstration of the Bernoulli Principle

There is a common demonstration of the Bernoulli principle that involves blowing across the top of a strip of paper held horizontally. Initially the paper hangs down in an arc, but when the blowing starts, the paper rises up. It is claimed that according to the Bernoulli principle, where the velocity is high the pressure is low. Therefore the paper moves toward the moving jet of air. This is completely wrong. This is not a valid application of the Bernoulli principle. The Bernoulli principle describes the conditions of air at two different cross sections of the same streamline. It postulates that energy is conserved as the air moves along a streamline, that the total energy is the same at both cross sections. The sum of the pressure energy and the kinetic energy is constant along the streamline, so when one goes up, the other goes down. This is summarized as “When the speed is high, the pressure is low and when the speed is low, the pressure is high.” You can’t apply that summary in a condition which is not consistent with the condition required by the Bernoulli principle. A wing is completely submerged in the air, with air moving above and below. In this demonstration that is not the case, we have a narrow jet of air moving over one surface with static air underneath. If you hold the strip of paper vertically and blow along one side, it does not move toward that side. Something else entirely is going on here.

This is a demonstration of Coanda effect. When the strip of paper is held horizontally the narrow jet of air is entrained on the top surface of a sheet which is hanging down in an arc. When a jet of air moves along an arc, it experiences a centrifugal force which pulls it outward. An entrained jet of air moving within an otherwise still surrounding atmosphere is nothing like a wing moving through the air.